Zadanie nr 9626159
Parametr 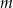 dobrano tak, że rozwiązaniem nierówności
dobrano tak, że rozwiązaniem nierówności
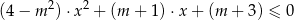
z niewiadomą  jest przedział postaci
jest przedział postaci 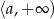 . Wynika stąd, że
. Wynika stąd, że
A) 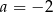 B)
B) 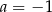 C)
C) 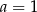 D)
D) 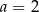
Rozwiązanie
Jeżeli rozwiązaniem danej nierówności jest przedział postaci 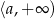 , to po jej lewej stronie musimy mieć funkcję liniową. Zatem
, to po jej lewej stronie musimy mieć funkcję liniową. Zatem

Otrzymujemy wtedy nierówność liniową
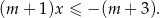
Jeżeli jej rozwiązaniem ma być przedział postaci 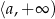 , to musi być
, to musi być 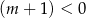 , czyli
, czyli 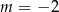 i mamy nierówność
i mamy nierówność
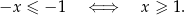
Zatem 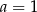 .
.
Odpowiedź: C

