Zadanie nr 5983209
Parametr 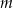 dobrano tak, że żadna liczba rzeczywista nie spełnia równania
dobrano tak, że żadna liczba rzeczywista nie spełnia równania
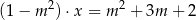
z niewiadomą  . Wynika stąd, że
. Wynika stąd, że
A) 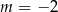 B)
B) 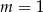 C)
C) 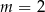 D)
D) 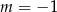
Rozwiązanie
Sposób I
Wiemy, że prosta
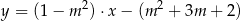
jest poziomą prostą różną od 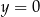 . Zatem
. Zatem
Z pierwszego równania otrzymujemy  . Łatwo sprawdzić, że tylko
. Łatwo sprawdzić, że tylko  spełnia drugą nierówność.
spełnia drugą nierówność.
Sposób II
Zauważmy, że
więc dane równanie możemy zapisać w postaci
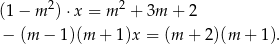
Widać teraz, że jeżeli 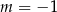 , to obie strony równania są stale równe zeru. Widać też, że dla
, to obie strony równania są stale równe zeru. Widać też, że dla 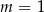 równanie jest sprzeczne, a dla
równanie jest sprzeczne, a dla 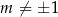 równanie ma dokładnie jedno rozwiązanie:
równanie ma dokładnie jedno rozwiązanie: 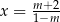 .
.
Odpowiedź: B

