Zadanie nr 2204857
Układ równań 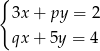 z niewiadomymi
z niewiadomymi  i
i 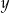 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 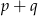 jest równa
jest równa
A) 6 B) 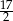 C)
C) 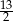 D) 15
D) 15
Rozwiązanie
Jeżeli układ ma mieć nieskończenie wiele rozwiązań, to proste odpowiadające równaniom układu muszą się pokrywać. To oznacza, że jedno równanie musi być wielokrotnością drugiego. Patrząc na prawe strony równań widzimy, że drugie równanie musi powstawać z pierwszego przez mnożenie przez 2. W takim razie 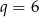 i
i 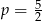 . Stąd
. Stąd
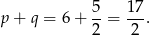
Odpowiedź: B

