Zadanie nr 9767410
Układ równań 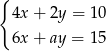 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 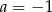 B)
B) 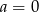 C)
C) 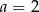 D)
D) 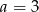
Rozwiązanie
Jeżeli układ ma mieć nieskończenie wiele rozwiązań to drugie równanie musi być wielokrotnością pierwszego. Ponieważ 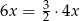 tak będzie, gdy
tak będzie, gdy
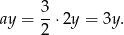
Zatem 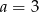 .
.
Odpowiedź: D

