Zadanie nr 2799386
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew. Po roku stwierdzono, że uschło 5% drzew w pierwszym sadzie i 10% drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano. Liczba drzew, które pozostały w drugim sadzie, stanowiła 60% liczby drzew, które pozostały w pierwszym sadzie. Niech  oraz
oraz 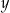 oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby
oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby  drzew posadzonych w pierwszym sadzie oraz liczby
drzew posadzonych w pierwszym sadzie oraz liczby 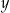 drzew posadzonych w drugim sadzie, jest
drzew posadzonych w drugim sadzie, jest
A) 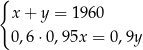 B)
B) 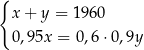
C) 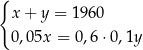 D)
D) 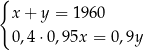
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

