/Szkoła średnia/Zadania testowe/Równania/Wymierne/Mianownik stopnia 1

Zadanie nr 6412492

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiązaniem równania 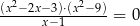(x2−2x−3)⋅(x2−9) x−1 = 0 nie jest liczba
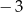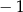A) − 3 B) − 1 C) 1 D) 3

Rozwiązanie

Sposób I

Rozłóżmy najpierw trójmian w pierwszym nawisie

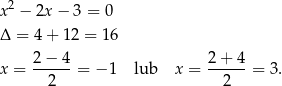
2 x − 2x − 3 = 0 Δ = 4 + 12 = 16 2 − 4 2 + 4 x = ------= − 1 lub x = ------= 3. 2 2

Zatem

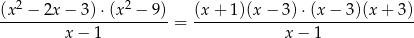
(x 2 − 2x − 3)⋅(x 2 − 9 ) (x + 1)(x − 3 )⋅(x − 3)(x + 3) ------------------------= ------------------------------- x − 1 x− 1

i rozwiązaniami danego równania są liczby 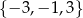{− 3 ,− 1 ,3 } .

Sposób II

Jeżeli popatrzymy na dane równanie i podane odpowiedzi, to widać, że rozwiązaniem na pewno nie jest 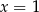x = 1 , bo dla takiej wartości x zeruje się wyrażenie w mianowniku.  
Odpowiedź: C

Wersja PDF