/Szkoła średnia/Zadania testowe/Równania/Wymierne/Mianownik stopnia 1

Zadanie nr 9392093

Równanie 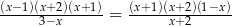(x−1)(x+2)(x+-1) (x+1)(x+-2)(1−x)- 3−x = x+ 2
A) ma cztery różne rozwiązania: 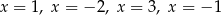x = 1, x = − 2, x = 3, x = − 1 .
B) ma trzy różne rozwiązania: 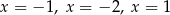x = − 1, x = − 2, x = 1 .
C) ma dwa różne rozwiązania: 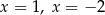x = 1, x = − 2 .
D) ma dwa różne rozwiązania: 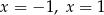x = − 1, x = 1 .

Wersja PDF

Rozwiązanie

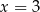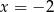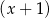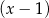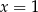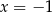Ze względu na mianowniki, na pewno rozwiązaniami równania nie są x = 3 i x = − 2 . Zauważmy też, że po obu stronach równania znajdują się czynniki (x + 1) i (x − 1 ) , więc liczby x = 1 i x = −1 są jego rozwiązaniami. Aby sprawdzić, czy nie ma innych rozwiązań dzielimy obie strony przez 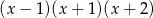(x − 1)(x + 1 )(x+ 2) . Otrzymujemy wtedy równanie

1 − 1 ------= ------ ⇐ ⇒ x − 3 = x+ 2, 3− x x+ 2

które jest oczywiście sprzeczne.  
Odpowiedź: D

Wersja PDF