/Szkoła średnia/Zadania testowe/Równania/Wymierne/Mianownik stopnia 2

Zadanie nr 1106750

Dodaj do ulubionych
Dodaj do rozwiązanych

Równanie

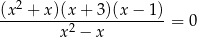
2 (x-+--x)(x+--3)(x-−-1)-= 0 x2 − x

ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 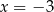x = − 3
B) dwa rozwiązania: 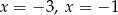x = − 3, x = − 1
C) trzy rozwiązania: 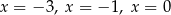x = −3 , x = − 1, x = 0
D) cztery rozwiązania: 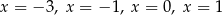x = − 3, x = − 1, x = 0, x = 1

Rozwiązanie

Równanie możemy zapisać w postaci

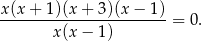
x(x + 1 )(x+ 3)(x− 1) ----------------------- = 0. x (x− 1)

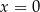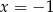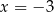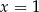Widać więc, że wyrażenia w liczniku zerują się dla x = 0 , x = − 1 , x = − 3 i x = 1 . Pierwsza i czwarta z tych liczb zeruje też mianownik – więc nie są to rozwiązania równania. Równanie ma zatem dwa rozwiązania: 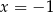x = − 1 i x = − 3 .  
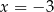Odpowiedź: B

Wersja PDF