Zadanie nr 2190159
Równanie 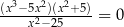 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Rozwiązanie
Zauważmy, że
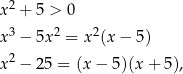
więc licznik zeruje się dla 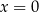 i
i 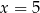 . Mianownik zeruje się dla
. Mianownik zeruje się dla 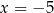 i
i 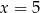 , więc
, więc 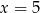 nie jest rozwiązaniem równania. Równanie ma więc tylko jedno rozwiązanie.
nie jest rozwiązaniem równania. Równanie ma więc tylko jedno rozwiązanie.
Odpowiedź: A

