/Szkoła średnia/Zadania testowe/Równania/Wymierne/Mianownik stopnia 2

Zadanie nr 8630598

Równanie 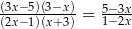(3x−5)(3−x-) 5−3x- (2x−1)(x+ 3) = 1−2x ma dwa rozwiązania. Są to liczby:
A) 3 i 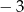− 3 B) 3 i 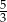5 3 C) 0 i 3 D) 0 i 5 3

Wersja PDF

Rozwiązanie

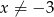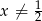Ze względu na wyrażenia w mianownikach musi oczywiście być x ⁄= − 3 i x ⁄= 12 . Przy tym założeniu możemy równanie przekształcić następująco.

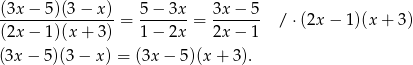
(3x-−-5)(3-−-x)-= 5-−-3x-= 3x-−-5- / ⋅(2x − 1)(x + 3) (2x − 1)(x + 3) 1 − 2x 2x − 1 (3x− 5)(3− x) = (3x − 5 )(x+ 3).

Widać teraz, że jednym z rozwiązań jest 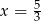5 x = 3 , a jeżeli 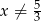5 x ⁄= 3 , to możemy obie strony równania podzielić przez 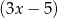(3x − 5) i mamy

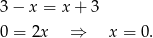
3 − x = x + 3 0 = 2x ⇒ x = 0.

 
Odpowiedź: D

Wersja PDF