Zadanie nr 1147051
Dana jest funkcja 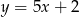 .
.
- Oblicz miejsce zerowe funkcji.
- Podaj współrzędne punktu przecięcia wykresu z osią
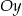 .
. - Oblicz wartość funkcji dla argumentu równego -2.
- Oblicz, dla jakiego argumentu wartość funkcji wynosi -3.
- Czy jest to funkcja rosnąca? Dlaczego?
Rozwiązanie
- Rozwiązujemy równanie
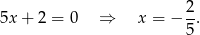
Odpowiedź: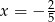
- Liczymy wartość w
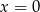 .
. 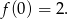
Odpowiedź: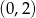
- Liczymy
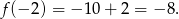
Odpowiedź: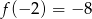
- Rozwiązujemy równanie
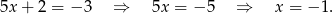
Odpowiedź: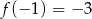
- Funkcja jest rosnąca, bo ma dodatni współczynnik kierunkowy.
Mówiąc bardziej wprost, jeżeli
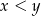 to
to 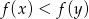 (widać to ze wzoru i łatwo uzasadnić), czyli dla większych argumentów funkcja przyjmuje większe wartości.
(widać to ze wzoru i łatwo uzasadnić), czyli dla większych argumentów funkcja przyjmuje większe wartości.
Odpowiedź: Tak, jest rosnąca.
Na koniec narysujmy wykres podanej funkcji.
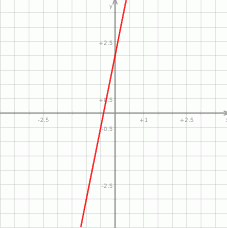
Fakt, że funkcja jest rosnąca widać na wykresie: jeżeli jedziemy w prawo wzdłuż osi  to wartości funkcji rosną (są coraz wyżej).
to wartości funkcji rosną (są coraz wyżej).

