Zadanie nr 1982448
Rozwiązaniem równania 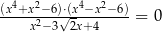 nie jest liczba
nie jest liczba
A) 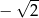 B)
B) 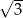 C)
C) 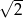 D)
D) 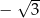
Rozwiązanie
Licznik wygląda na dość skomplikowany, ale w mianowniku mamy zwykły trójmian kwadratowy – sprawdźmy jakie są jego miejsca zerowe.
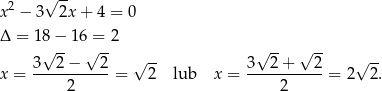
To oznacza, że 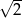 na pewno nie jest rozwiązaniem danego równania (bo dla tej liczby otrzymujemy zero w mianowniku). Można też sprawdzić (choć oczywiście nie musimy tego robić), że każda z pozostałych odpowiedzi jest rozwiązaniem danego równania.
na pewno nie jest rozwiązaniem danego równania (bo dla tej liczby otrzymujemy zero w mianowniku). Można też sprawdzić (choć oczywiście nie musimy tego robić), że każda z pozostałych odpowiedzi jest rozwiązaniem danego równania.
Odpowiedź: C

