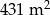/Szkoła średnia/Zadania z treścią/Geometryczne/Pole powierzchni

Zadanie nr 4363249

Dodaj do ulubionych
Dodaj do rozwiązanych

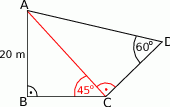
Pan Piotrek ma działkę w kształcie czworokąta, jak na rysunku. Oblicz powierzchnię tej działki. Wynik zaokrąglij do 1 m.

PIC

Rozwiązanie

Obliczamy długość boku 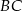BC

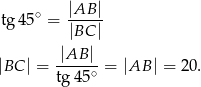
|AB | tg 45∘ = ----- |BC | |AB | |BC | = -----∘ = |AB | = 20. tg4 5

Zatem

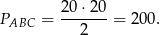
2 0⋅20 PABC = -------= 200. 2

Z twierdzenia Pitagorasa wyznaczamy długość odcinka 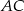AC

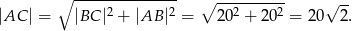
∘ -------------- 2 2 ∘ --2-----2- √ -- |AC | = |BC | + |AB | = 20 + 20 = 20 2 .

Wyznaczamy długość odcinka 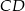CD

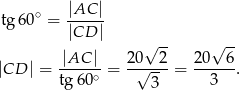
tg60∘ = |AC-| |CD | √ -- √ -- |CD | = |AC-|-= 20√--2-= 20---6. tg60∘ 3 3

Obliczamy pole powierzchni

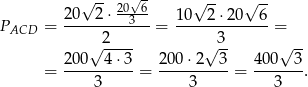
√ -- √- √ -- √ -- 20 2 ⋅ 2036 10 2 ⋅20 6 PACD = ------------= -------------= √ 2--- √ 3- √ -- 200--4-⋅3- 200-⋅2--3- 400--3- = 3 = 3 = 3 .

Wykonujemy obliczenia pomocnicze

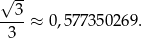
√ -- --3- 3 ≈ 0,5773 50269.

Zatem pole działki wynosi

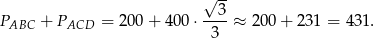
√ -- --3- PABC + PACD = 200 + 400 ⋅ 3 ≈ 200 + 231 = 431.

 
Odpowiedź: 431 m 2

Wersja PDF