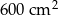/Szkoła średnia/Zadania z treścią/Geometryczne/Pole powierzchni

Zadanie nr 5549219

Dodaj do ulubionych
Dodaj do rozwiązanych

Działka budowlana Andrzeja ograniczona jest dwiema równoległymi alejami i dwoma innymi lokalnymi drogami. Andrzej zmierzył odcinki alei ograniczające działki (80 m i 20 m) oraz długości dwóch ścieżek znajdujących się na terenie tej działki, łączących jej przeciwległe rogi (80 m i 60 m). Następnie wykonał plan tej działki w skali 1:200 i wyznaczył pole powierzchni planu działki. Ile ono wynosiło?

PIC

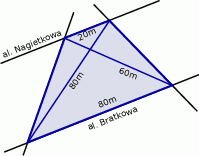
Rozwiązanie

Zacznijmy od podpisania punktów na rysunku.

PIC

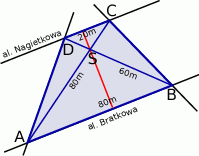
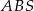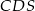Trójkąty ABS i CDS mają takie same kąty, więc są podobne. W dodatku wiemy, że ich skala podobieństwa jest równa

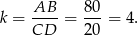
k = AB--= 80-= 4. CD 20

Zatem

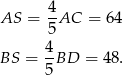
AS = 4AC = 64 5 4- BS = 5BD = 48.

Zastanówmy się co będziemy dalej liczyć. Do wyliczenia pola trapezu brakuje nam jego wysokości. Z zauważonego podobieństwa, wystarczy wyznaczyć wysokość trójkąta 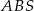ABS . Można to zrobić następująco: ze wzoru Herona wyliczymy pole trójkąta 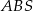ABS , a potem ze wzoru na pole wyliczymy jego wysokość. Liczymy

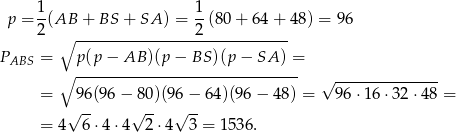
p = 1(AB + BS + SA ) = 1-(80 + 64 + 4 8) = 96 2 ∘ ----------------2------------ PABS = p(p − AB )(p − BS )(p − SA ) = ∘ ------------------------------- √ -------------- = 96(9 6− 80)(96− 64)(96 − 48) = 96⋅ 16⋅3 2⋅48 = √ -- √ -- √ -- = 4 6 ⋅4⋅4 2⋅4 3 = 1536 .

Możemy teraz wyliczyć długość wysokości trójkąta 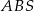ABS . Od razu zapiszemy, że jest ona równa 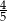4 5 wysokości trapezu h .

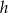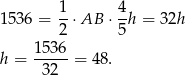
1 4 15 36 = --⋅AB ⋅--h = 32h 2 5 h = 1536-= 48. 32

Zatem pole trapezu jest równe

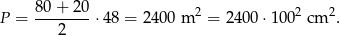
P = 80+--20-⋅48 = 24 00 m 2 = 2400 ⋅1002 cm 2. 2

Aby otrzymać pole w zadanej skali, musimy podzielić tę liczbę przez 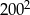2 2 00 . Zatem szukane pole jest równe

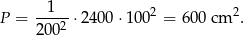
P = --1--⋅2 400⋅ 1002 = 600 cm 2. 200 2

 
Odpowiedź: 600 cm 2

Wersja PDF