/Szkoła średnia/Zadania z treścią/Geometryczne/Pole powierzchni

Zadanie nr 7754559

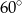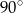Boja ma kształt dwóch stożków połączonych podstawami, przy czym kąty rozwarcia tych stożków są równe 6 0∘ i 90∘ , a odległość ich wierzchołków jest równa 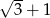√ -- 3 + 1 . Oblicz pole powierzchni tej boi.

PIC

Wersja PDF

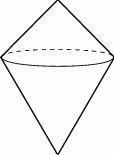
Rozwiązanie

Oczywiście wystarczy zajmować się przekrojem osiowym.

PIC

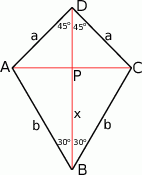
Sposób I

Zauważmy, że trójkąt 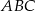ABC jest równoboczny, więc przy oznaczeniach z rysunku mamy

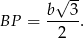
√ -- b--3- BP = 2 .

Ponadto trójkąt 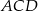ACD jest połówką kwadratu, więc

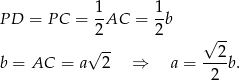
P D = P C = 1AC = 1b 2 2 √ -- √ 2- b = AC = a 2 ⇒ a = ----b. 2

Z podanej długości 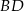BD mamy

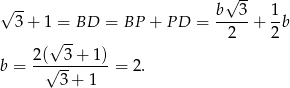
√ -- √ -- 3 + 1 = BD = BP + PD = b--3-+ 1-b √ -- 2 2 2( 3+ 1) b = -√---------= 2. 3 + 1

Zatem promień podstawy stożków jest równy 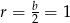b r = 2 = 1 , oraz 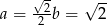√-2 √ -- a = 2 b = 2 . Liczymy pole powierzchni bocznej.

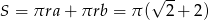
√ -- S = πra + πrb = π( 2 + 2)

Sposób II

Jeżeli oznaczymy 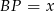BP = x to mamy

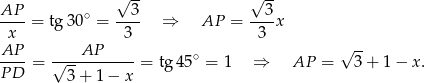
√ -- √ -- AP-- ∘ --3- --3- x = tg30 = 3 ⇒ AP = 3 x AP AP √ -- ----= √-----------= tg 45∘ = 1 ⇒ AP = 3 + 1 − x . P D 3 + 1 − x

Mamy stąd

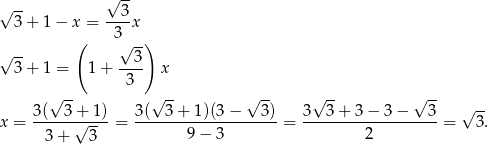
-- √ -- √ 3+ 1− x = --3-x 3 √ -- ( √ -) 3+ 1 = 1+ --3- x 3 √ -- √ -- √ -- √ -- √ -- -- x = 3(--3-+√-1)-= 3(--3-+-1)(3-−---3)-= 3--3-+-3-−-3-−---3-= √ 3. 3+ 3 9 − 3 2

Zatem

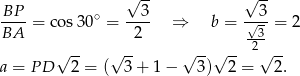
√ -- √ -- BP-- ∘ --3- --3- BA = co s30 = 2 ⇒ b = √-3 = 2 √ -- √ -- √ -- √ -- 2√ -- a = PD 2 = ( 3 + 1 − 3 ) 2 = 2.

Pole powierzchni liczymy jak poprzednio.

Sposób III

Tym razem popatrzmy na trójkąt 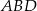ABD – znamy jego dwa kąty i bok, a chcemy wyliczyć długości pozostałych boków. Łatwo to zrobić z twierdzenia sinusów, o ile tylko wyliczymy sinus kąta 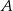A . Liczymy

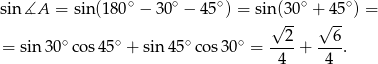
sin ∡A = sin(18 0∘ − 30∘ − 45∘) = sin(30∘ + 45∘ ) = √ -- √ -- ∘ ∘ ∘ ∘ --2- --6- = sin3 0 cos 45 + sin 45 cos 30 = 4 + 4 .

Korzystamy teraz z twierdzenia sinusów

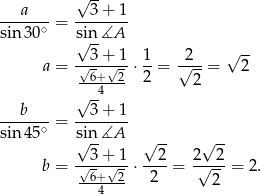
√ -- ---a--- = --3+-1-- sin 30∘ s√in-∡A 3+ 1 1 2 √ -- a = √6+-√2-⋅ --= √----= 2 ---4--- 2 2 b √ 3+ 1 ------- = -------- sin 45∘ s√in-∡A √ -- √ -- 3+ 1 2 2 2 b = √6+-√2-⋅ ----= √----= 2. ---4--- 2 2

Pole powierzchni liczymy jak poprzednio.  
Odpowiedź: √ -- π ( 2+ 2)

Wersja PDF