/Szkoła średnia/Zadania z treścią/Geometryczne/Pole powierzchni

Zadanie nr 8496247

Działkę w kształcie trapezu podzielono przekątnymi na 4 działki. Spośród tych czterech działek wskaż dwie o równych polach. Odpowiedź uzasadnij.

Wersja PDF

Rozwiązanie

Robimy rysunek.

PIC

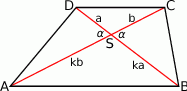
Uzasadnimy na dwa sposoby, że działki o równych polach to 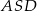ASD i BSC .

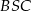Sposób I

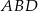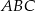Zauważmy, że trójkąty ABD i ABC mają wspólną podstawę 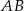AB oraz wysokości opuszczone na tę podstawę mają w obu trójkątach tę samą długość (jest to po prostu odległość między podstawami trapezu). Zatem mają równe pola, czyli

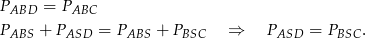
PABD = PABC PABS + PASD = PABS + PBSC ⇒ PASD = PBSC.

Sposób II

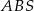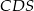Tym razem skorzystamy ze wzoru na pole z sinusem. Zauważmy, że trójkąty ABS i CDS są podobne (bo mają równe kąty). Jeżeli oznaczymy skalę ich podobieństwa przez 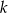k to mamy

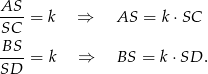
AS--= k ⇒ AS = k ⋅SC SC BS-- SD = k ⇒ BS = k⋅SD .

Teraz wystarczy zauważyć, że

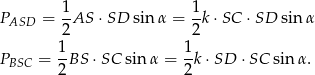
1 1 PASD = 2AS ⋅SD sin α = 2k ⋅SC ⋅SD sinα PBSC = 1-BS ⋅SC sin α = 1k ⋅SD ⋅ SC sin α. 2 2

Zatem rzeczywiście 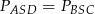PASD = PBSC .

Wersja PDF