/Szkoła średnia/Zadania z treścią/Geometryczne/Długość i odległość

Zadanie nr 5205931

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwie szkoły wybudowały boiska do piłki nożnej. Powierzchnia pierwszego ma 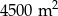45 00 m 2 . Drugie boisko jest o 10 metrów szersze oraz 20 metrów dłuższe od pierwszego i ma powierzchnię 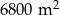6800 m 2 . Podaj wymiary obu boisk szkolnych. Uwzględnij wymaganie, że boisko piłkarskie musi mieć kształt prostokąta, ale nie może być kwadratem. Długość boiska do piłki nożnej nie może przekraczać 120 metrów ani być mniejsza niż 70 metrów. Musi też być w każdym przypadku dłuższa od szerokości boiska, która ma mieścić się w przedziale od 45 m do 90 m.

Rozwiązanie

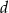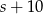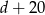Oznaczmy szerokość i długość pierwszego boiska przez s i d . W takim razie drugie boisko ma wymiary s+ 10 i d + 20 i otrzymujemy układ równań

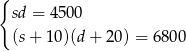
{ sd = 450 0 (s+ 10)(d+ 20) = 68 00

Przekształćmy drugie równanie korzystając z równości 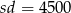sd = 4500 .

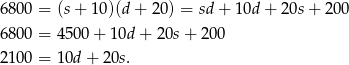
6800 = (s+ 10)(d+ 20) = sd + 10d + 2 0s+ 2 00 6800 = 4500 + 10d + 2 0s+ 2 00 2100 = 10d + 20s.

Podstawiamy teraz do tej równości 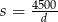4500 s = d .

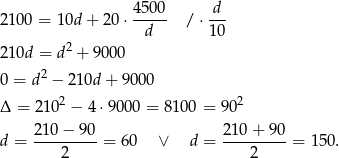
4500 d 2100 = 1 0d+ 20 ⋅----- / ⋅--- d 10 210d = d2 + 9000 2 0 = d − 210d + 9 000 Δ = 2102 − 4⋅9 000 = 810 0 = 902 d = 21-0−--90 = 60 ∨ d = 21-0+-9-0 = 150 . 2 2

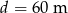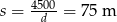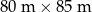Ponieważ długość boiska nie może przekraczać 120 metrów, drugie rozwiązanie odrzucamy i mamy d = 60 m . Wtedy s = 450d0-= 75 m . Drugie boisko ma więc wymiary 80 m × 85 m .  
Odpowiedź: 60 m na 75 m i 80 m na 85 m

Wersja PDF