Zadanie nr 2309532
Ze środka górnej ściany sześcianu wypuszczono promień świetlny, który odbija się od ścian sześcianu zgodnie z zasadą „kąt padania jest równy kątowi odbicia”. Promień porusza się w płaszczyźnie prostopadłej do jednej ze ścian sześcianu oraz został wypuszczony pod kątem 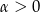 wględem prostej prostopadłej do górnej ściany sześcianu i przechodzącej przez jej środek. Dla jakich wartości
wględem prostej prostopadłej do górnej ściany sześcianu i przechodzącej przez jej środek. Dla jakich wartości 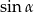 promień odbije się od bocznej ściany sześcianu, a potem trafi w dolną ścianę sześcianu?
promień odbije się od bocznej ściany sześcianu, a potem trafi w dolną ścianę sześcianu?
Rozwiązanie
Narysujmy sobie przekrój sześcianu płaszczyzną, w której porusza się promień i oznaczmy długość krawędzi sześcianu przez  .
.
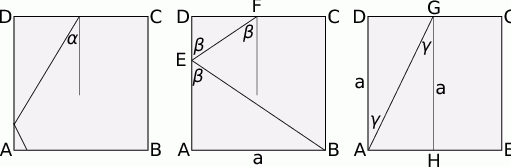
Jak się chwilę zastanowimy to widać, że są dwie skrajne sytuacje: gdy promień po odbiciu od bocznej ściany trafia w wierzchołek 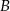 , oraz gdy promień od razu trafia w wierzchołek
, oraz gdy promień od razu trafia w wierzchołek 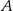 . Spróbujemy ustalić jakie są sinusy tych skrajnych kątów
. Spróbujemy ustalić jakie są sinusy tych skrajnych kątów 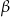 i
i 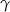 .
.
Zauważmy, że trójkąty 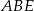 i
i 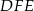 są podobne, oraz ich skala podobieństwa wynosi
są podobne, oraz ich skala podobieństwa wynosi
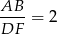
Zatem
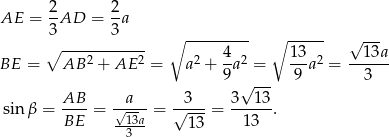
Teraz zajmijmy się kątem 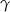 . Mamy
. Mamy
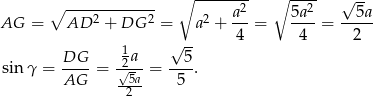
Kąt  musi być pomiędzy
musi być pomiędzy 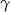 a
a 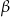 , zatem
, zatem
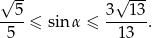
Odpowiedź: