Zadanie nr 2136689
Samochód 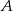 , jadący pod górę, w pierwszej sekundzie pokonał 25 m, a w każdej następnej o pół metra mniej niż w poprzedniej. W tym samym momencie, gdy
, jadący pod górę, w pierwszej sekundzie pokonał 25 m, a w każdej następnej o pół metra mniej niż w poprzedniej. W tym samym momencie, gdy 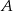 rozpoczął podjazd, zjazd z góry rozpoczął samochód
rozpoczął podjazd, zjazd z góry rozpoczął samochód 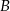 , będący w odległości 360 m od
, będący w odległości 360 m od 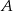 . Samochód
. Samochód 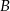 w pierwszej sekundzie przebył drogę 9 m, a w każdej następnej o 2 m więcej niż w poprzedniej. Jaką odległość pokonał samochód
w pierwszej sekundzie przebył drogę 9 m, a w każdej następnej o 2 m więcej niż w poprzedniej. Jaką odległość pokonał samochód 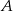 do chwili minięcia z samochodem
do chwili minięcia z samochodem 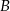 ?
?
Rozwiązanie
Sposób I
Policzmy jaką drogę przebył każdy z samochodów w czasie 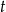 sekund. Droga pokonana przez samochód
sekund. Droga pokonana przez samochód 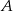 jest sumą malejącego ciągu arytmetycznego z
jest sumą malejącego ciągu arytmetycznego z 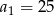 i
i 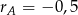 , a droga samochodu
, a droga samochodu 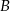 jest sumą rosnącego ciągu z
jest sumą rosnącego ciągu z 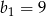 i
i 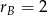 . Zatem po
. Zatem po 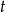 sekundach samochody przejechały
sekundach samochody przejechały
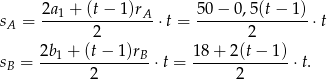
Samochody się spotkają, gdy w sumie przejadą 360 m, czyli
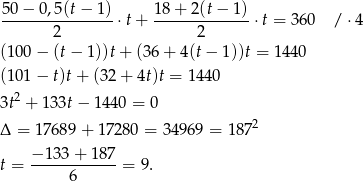
Samochody spotkały się więc po 9 sekundach. Samochód 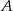 przebył w tym czasie drogę
przebył w tym czasie drogę
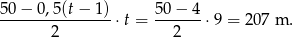
Sposób II
Zadanie można też rozwiązać wprost, bez używania żadnych wzorów. Zróbmy tabelkę z odległościami pokonanymi przez oba samochody (można zauważyć, że samochody zbliżają się coraz szybciej, więc tabelka nie będzie zbyt długa).
| Sekunda | Droga A | Droga A w sumie | Droga B | Droga B w sumie | Razem |
| 1 | 25 | 25 | 9 | 9 | 34 m |
| 2 | 24,5 | 49,5 | 11 | 20 | 69,5 m |
| 3 | 24 | 73,5 | 13 | 33 | 106,5 m |
| 4 | 23,5 | 97 | 15 | 48 | 145 m |
| 5 | 23 | 120 | 17 | 65 | 185 m |
| 6 | 22,5 | 142,5 | 19 | 84 | 222,5 m |
| 7 | 22 | 164,5 | 21 | 105 | 269,5 m |
| 8 | 21,5 | 186 | 23 | 128 | 314 m |
| 9 | 21 | 207 | 25 | 153 | 360 m |
No i dalej możemy nie liczyć, bo widać, że po 9 sekundach samochody się spotkały. Samochód 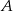 przejechał w tym czasie 207 m.
przejechał w tym czasie 207 m.
Odpowiedź: 207 metrów

