/Szkoła średnia/Zadania z treścią/Prędkość/2 ruchome obiekty

Zadanie nr 3406331

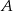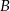Z miejscowości A i B , które są odległe o 58,5 km wyruszyły jednocześnie ku sobie dwa samochody. Pierwszy samochód w ciągu pierwszej minuty jechał ze średnią prędkością 30 km/h, a w ciągu każdej następnej minuty pokonywał drogę o 0,25 km dłuższą, niż w ciągu poprzedniej minuty. Drugi samochód przez pierwsze 6 minut przejechał 21 kilometrów, a potem jechał ze stałą prędkością 150 km/h. Oblicz po ilu minutach nastąpi spotkanie samochodów.

Wersja PDF

Rozwiązanie

Pierwszy samochód w ciągu pierwszej minuty przejechał

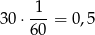
1 3 0⋅ ---= 0,5 60

kilometra. Ponadto wiemy, że w każdej następnej minucie przejeżdża o 0,25 km więcej, więc w n -tej minucie przejechał

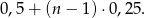
0,5 + (n − 1) ⋅0,25.

Ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego wiemy, że po n minutach przejechał

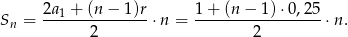
S = 2a1-+-(n-−-1)r-⋅n = 1+--(n−--1)⋅-0,25-⋅n. n 2 2

Zajmijmy się teraz drugim samochodem. Wiemy, że w ciągu pierwszych 6 minut przejechał 21 kilometrów, a potem przejeżdża

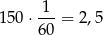
150 ⋅-1-= 2,5 60

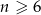kilometra w ciągu 1 minuty. Zatem po n minutach (jeżeli n ≥ 6 ) przejedzie

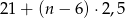
2 1+ (n − 6)⋅2,5

kilometrów.

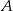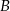Samochody spotkają się, jeżeli w sumie przejadą dystans dzielący miejscowości A i B , czyli 58, 5 km. Daje to nam równanie

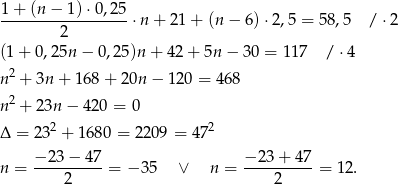
1-+-(n-−-1)-⋅0,25- 2 ⋅n + 21 + (n − 6) ⋅2,5 = 5 8,5 / ⋅2 (1+ 0,25n − 0,25 )n + 42+ 5n − 30 = 1 17 / ⋅4 n2 + 3n + 168 + 20n − 120 = 46 8 2 n + 23n − 420 = 0 Δ = 2 32 + 1680 = 22 09 = 472 n = −-23-−-4-7 = − 35 ∨ n = −-23-+-47-= 12. 2 2

Ujemną odpowiedź odrzucamy i mamy 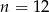n = 12 .  
Odpowiedź: Po 12 minutach.

Wersja PDF