Zadanie nr 9140631
Z dwóch miast 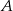 i
i 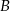 , odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta
, odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj turyści. Pierwszy turysta wyszedł z miasta 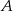 o jedną godzinę wcześniej niż drugi z miasta
o jedną godzinę wcześniej niż drugi z miasta 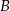 . Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta
. Oblicz prędkość, z jaką szedł każdy turysta, jeżeli wiadomo, że po spotkaniu pierwszy turysta szedł do miasta 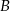 jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta
jeszcze 1,5 godziny, drugi zaś szedł jeszcze 4 godziny do miasta 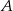 .
.
Rozwiązanie
Oznaczmy przez 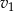 i
i 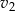 odpowiednio prędkości pierwszego i drugiego turysty, a przez
odpowiednio prędkości pierwszego i drugiego turysty, a przez 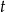 czas po jakim pierwszy turysta spotkał drugiego turystę. Do momentu spotkania pierwszy turysta przeszedł więc
czas po jakim pierwszy turysta spotkał drugiego turystę. Do momentu spotkania pierwszy turysta przeszedł więc 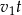 , a drugi
, a drugi 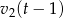 kilometrów. W sumie przeszli do tego momentu całą odległość między miastami, co daje równanie.
kilometrów. W sumie przeszli do tego momentu całą odległość między miastami, co daje równanie.
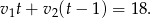
Wiemy ponadto, że pokonanie pozostałych 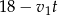 kilometrów zajęło pierwszemu turyście 1,5 godziny, a pokonanie pozostałych
kilometrów zajęło pierwszemu turyście 1,5 godziny, a pokonanie pozostałych 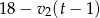 kilometrów zajęło drugiemu turyście 4 godziny. Otrzymujemy stąd dwa kolejne równania.
kilometrów zajęło drugiemu turyście 4 godziny. Otrzymujemy stąd dwa kolejne równania.
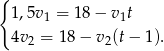
Otrzymany układ trzech równań można rozwiązań na różne sposoby, my wyliczymy z dwóch ostatnich równań 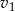 i
i 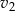 w zależności od
w zależności od 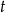 i podstawimy otrzymane wyrażenia do pierwszego z otrzymanych równań. Liczymy
i podstawimy otrzymane wyrażenia do pierwszego z otrzymanych równań. Liczymy
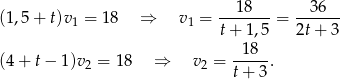
Podstawiamy do pierwszego równania
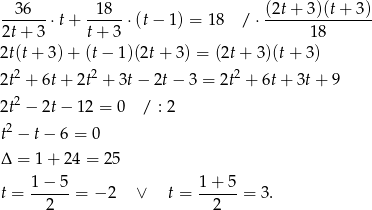
Ujemne rozwiązanie odrzucamy i mamy 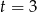 . Stąd
. Stąd
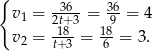
Odpowiedź: 4 km/h i 3 km/h

