Zadanie nr 9654034
Miasta 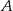 i
i 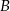 są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości:
są odległe o 450 km. Pani Danuta pokonała tę trasę swym samochodem w czasie o 75 minut dłuższym niż pani Lidia. Wartość średniej prędkości, z jaką jechała pani Danuta na całej trasie, była o 18 km/h mniejsza od wartości średniej prędkości, z jaką jechała pani Lidia. Oblicz średnie wartości:
– prędkości, z jaką pani Danuta jechała z A do B.
– prędkości, z jaką pani Lidia jechała z A do B.
Rozwiązanie
Sposób I
Niech 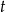 i
i  oznaczają odpowiednio czas przejazdu oraz prędkość pani Lidii. Z założeń mamy
oznaczają odpowiednio czas przejazdu oraz prędkość pani Lidii. Z założeń mamy
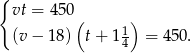
Podstawiamy 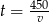 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
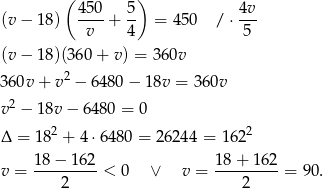
Ujemne rozwiązanie odrzucamy i mamy 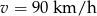 . Wtedy prędkość pani Danuty to
. Wtedy prędkość pani Danuty to
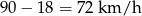
Sposób II
Wprowadzamy oznaczenia: 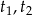 niech oznaczają czas przejazdu pani Lidii i pani Danuty, a
niech oznaczają czas przejazdu pani Lidii i pani Danuty, a 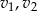 niech oznaczają ich prędkości. Z założeń mamy
niech oznaczają ich prędkości. Z założeń mamy
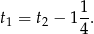
Stąd
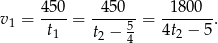
Podstawiamy to do równania
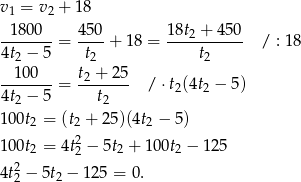
Wyznaczamy pierwiastki
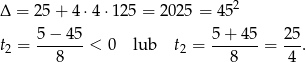
Obliczamy prędkość Pani Danuty
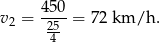
Teraz pozostało nam tylko obliczyć prędkość pani Lidii
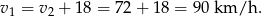
Odpowiedź: Prędkość pani Danuty: 72 km/h, pani Lidii: 90 km/h.

