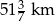Zadanie nr 9932208
Z dwóch miast 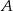 i
i 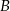 odległych od siebie o 90 km wyjechali rowerami dwaj znajomi, by spotkać się o umówionej godzinie w miejscowości
odległych od siebie o 90 km wyjechali rowerami dwaj znajomi, by spotkać się o umówionej godzinie w miejscowości 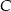 , znajdującej się między
, znajdującej się między 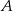 i
i 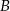 . Pierwszy (z
. Pierwszy (z 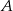 ) wyjechał o godzinę później niż drugi. W jakiej odległości od
) wyjechał o godzinę później niż drugi. W jakiej odległości od 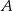 znajduje się
znajduje się 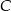 , jeśli wiemy, że gdyby znajomi kontynuowali podróż (po spotkaniu w
, jeśli wiemy, że gdyby znajomi kontynuowali podróż (po spotkaniu w 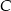 ), każdy w wybranym wcześniej kierunku i z dotychczasową szybkością, to pierwszy dotarłby do
), każdy w wybranym wcześniej kierunku i z dotychczasową szybkością, to pierwszy dotarłby do 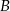 po półtorej godziny, zaś drugi do
po półtorej godziny, zaś drugi do 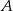 – po 4 godzinach?
– po 4 godzinach?
Rozwiązanie
Oznaczmy przez 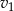 i
i 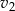 odpowiednio prędkości pierwszego i drugiego znajomego, a przez
odpowiednio prędkości pierwszego i drugiego znajomego, a przez 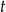 czas po jakim pierwsza osoba dotarła do
czas po jakim pierwsza osoba dotarła do 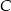 . Do momentu spotkania pierwsza osoba przejechała więc
. Do momentu spotkania pierwsza osoba przejechała więc 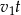 , a druga
, a druga 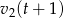 kilometrów. W sumie przejechali do tego momentu całą odległość między
kilometrów. W sumie przejechali do tego momentu całą odległość między 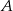 i
i 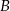 , co daje równanie.
, co daje równanie.
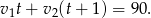
Wiemy ponadto, że pokonanie pozostałych 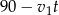 kilometrów zajęło pierwszemu turyście 1,5 godziny, a pokonanie pozostałych
kilometrów zajęło pierwszemu turyście 1,5 godziny, a pokonanie pozostałych 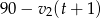 kilometrów zajęło drugiemu turyście 4 godziny. Otrzymujemy stąd dwa kolejne równania.
kilometrów zajęło drugiemu turyście 4 godziny. Otrzymujemy stąd dwa kolejne równania.
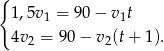
Otrzymany układ trzech równań można rozwiązań na różne sposoby, my wyliczymy z dwóch ostatnich równań 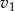 i
i 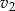 w zależności od
w zależności od 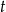 i podstawimy otrzymane wyrażenia do pierwszego z otrzymanych równań. Liczymy
i podstawimy otrzymane wyrażenia do pierwszego z otrzymanych równań. Liczymy
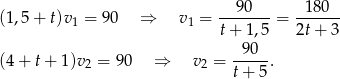
Podstawiamy do pierwszego równania
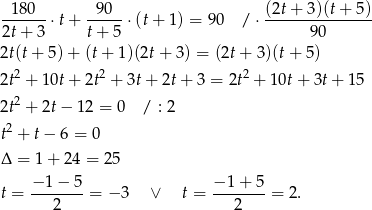
Ujemne rozwiązanie odrzucamy i mamy 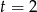 . Stąd
. Stąd
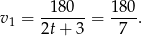
Odległość między miastami  i
i 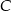 jest więc równa
jest więc równa
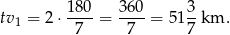
Sposób II
Tym razem za niewiadome przyjmijmy czas 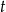 po jakim pierwsza osoba dojechała do
po jakim pierwsza osoba dojechała do 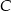 oraz odległość
oraz odległość  między
między 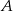 i
i 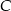 . Zauważmy teraz, że możemy na dwa sposoby obliczyć prędkość pierwszej osoby:
. Zauważmy teraz, że możemy na dwa sposoby obliczyć prędkość pierwszej osoby:
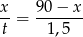
(po prawej stronie liczymy prędkość uwzględniając podaną informację o czasie w jakim pierwsza osoba przejechała pozostałe 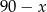 kilometrów). Podobnie, na dwa sposoby liczymy prędkość drugiej osoby (pamiętajmy, że startuje ona z
kilometrów). Podobnie, na dwa sposoby liczymy prędkość drugiej osoby (pamiętajmy, że startuje ona z 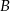 ):
):
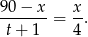
Podstawiamy teraz 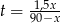 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
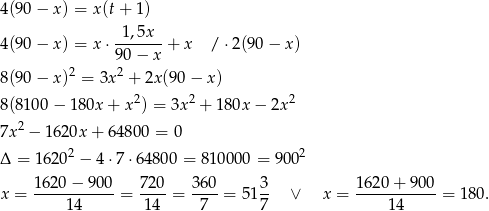
Drugie rozwiązanie odpada, bo odległość od 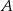 do
do 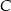 nie może być większa niż 90 km, więc
nie może być większa niż 90 km, więc 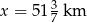 .
.
Odpowiedź: