Zadanie nr 7471512

Z murów zamku wystrzelono pocisk armatni, który po 4 sekundach spadł na ziemię. Wysokość (w metrach), na jaką wzniósł się pocisk (względem poziomu armaty) po upływie 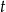sekund od momentu wystrzelenia opisuje funkcja 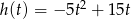h(t) = − 5t2 + 15t , gdzie t ∈ ⟨0,4 ⟩ .

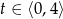Oblicz po jakim czasie pocisk ponownie znalazł się na wysokości z jakiej został wystrzelony.
Oblicz na jaką maksymalną wysokość względem ziemi wzniósł się ten pocisk.

Rozwiązanie

Skoro funkcja 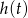opisuje położenie (wysokość) pocisku względem miejsca wystrzelenia, musimy rozwiązać równanie .
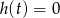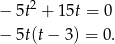
$− 5t2 + 15t = 0 − 5t(t− 3) = 0.$

Pierwiastek 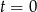odpowiada chwili wystrzału, więc mamy .
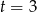Odpowiedź: Po 3 sekundach.
Wykresem funkcji 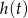jest parabola o ramionach skierowanych w dół, więc maksymalną wysokość otrzymamy w wierzchołku, czyli dla 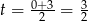(dokładnie w środku między pierwiastkami). Wartość ta jest równa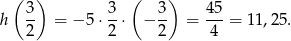
$( ) ( ) 3- 3- 3- 45- h 2 = − 5 ⋅2 ⋅ − 2 = 4 = 1 1,25.$

To co wyliczyliśmy to jednak wysokość względem miejsca wystrzelenia, a mieliśmy obliczyć wysokość względem ziemi. Wysokość na jakiej znajduje się armata możemy wyznaczyć, sprawdzając na jakiej (względnej) wysokości znajduje się pocisk w chwili .

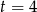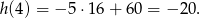
$h(4) = − 5 ⋅16 + 60 = −2 0.$

Zatem armata znajduje się na wysokości 20 m, a maksymalna wysokość pocisku to

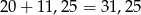
$20 + 11,25 = 31,25$

metra.
Odpowiedź: 31,25 m