/Szkoła średnia/Zadania z treścią/Prędkość/Inne

Zadanie nr 5052176

W rajdzie motocyklowym zawodnik, który zwyciężył, przejechał trasę z prędkością o 20 km/h większą niż drugi zawodnik i o 25 km/h większą od trzeciego zawodnika. Zawodnicy wystartowali jednocześnie. Na mecie drugi zawodnik był o 18 minut później niż zwycięzca i o 6 minut wcześniej niż trzeci zawodnik. Oblicz:

  • długość trasy rajdu;
  • prędkość jazdy każdego zawodnika;
  • czasy przejazdu tych zawodników.
Wersja PDF

Rozwiązanie

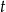  • Niech v będzie prędkością najwolniejszego zawodnika, s długością trasy, a t czasem w jakim najwolniejszy zawodnik pokonał całą trasę. Mamy zatem układ równań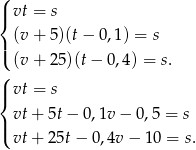
    ( |{ vt = s (v + 5)(t− 0,1) = s |( (v + 25)(t− 0,4) = s. ( |{ vt = s | vt+ 5t− 0 ,1v− 0,5 = s ( vt+ 25t− 0,4v− 10 = s.

    Uwzględniając pierwsze równanie w drugim i trzecim otrzymujemy

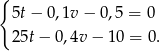
    { 5t − 0,1v − 0,5 = 0 25t − 0,4v − 1 0 = 0.

    Od drugiego równania odejmujemy pierwsze pomnozone przez 4 (żeby skrócić v ) i mamy

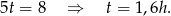
    5t = 8 ⇒ t = 1,6h .

    Stąd v=75km/h i s=120km.  
    Odpowiedź: s=120km

  • Z poprzedniego podpunktu mamy prędkości: 75km/h, 80km/h i 100km/h.  
    Odpowiedź: 75km/h, 80km/h i 100km/h
  • Czasy wynoszą 1,6h, 1,5h i 1,2h.  
    Odpowiedź: 1,6h, 1,5h i 1,2h
Wersja PDF