/Szkoła średnia/Zadania z treścią/Praca i moc

Zadanie nr 3539769

Do basenu zawierającego 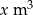3 x m wody doprowadzono pierwszego dnia 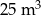3 25 m wody, po czym każdego dnia doprowadzano o 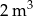2 m 3 wody więcej niż dnia poprzedniego. Równocześnie z basenu ubywa codziennie 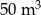5 0 m 3 wody.

  • Jaka musi być początkowa ilość wody w basenie, aby w tych warunkach basen nigdy nie został opróżniony?
  • Po ilu dniach basen będzie zawierał najmniejszą ilość wody?
Wersja PDF

Rozwiązanie

Z podanych informacji wynika, że n -tego dnia ilość wody w basenie zmienia się o

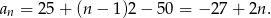
an = 25 + (n − 1)2 − 50 = − 2 7+ 2n .

Zauważmy, że liczba ta zaczyna być dodatnia dla 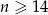n ≥ 14 . Zatem najmniejsza ilość wody w basenie będzie po 13 dniach. Aby basen nie został opróżniony, ilość wylanej wody musi być mniejsza niż początkowa ilość wody w basenie, czyli

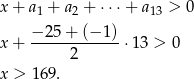
x+ a + a + ⋅⋅ ⋅+ a > 0 1 2 13 −-25-+-(−-1)- x+ 2 ⋅13 > 0 x > 169.

 
Odpowiedź: Więcej niż 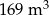169 m 3 . Po 13 dniach.

Wersja PDF