Zadanie nr 4533485
Woda może wpływać do basenu z dwóch kranów. Za pomocą pierwszego kranu basen można napełnić w czasie o 2 godziny dłuższym, a za pomocą drugiego kranu w czasie o 4,5 godziny dłuższym, niż przy napełnianiu basenu z wykorzystaniem obu kranów. W jakim czasie można napełnić ten basen odkręcając tylko pierwszy albo tylko drugi kran?
Rozwiązanie
Sposób I
Powiedzmy, że napełnianie basenu kranami pierwszym i drugim trwa odpowiednio 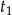 i
i 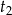 godzin. Zatem w ciągu 1 godziny krany zapełniają odpowiednio
godzin. Zatem w ciągu 1 godziny krany zapełniają odpowiednio 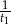 i
i 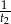 część objętości basenu. Jeżeli są odkręcone oba krany na raz, to w ciągu godziny napełniają
część objętości basenu. Jeżeli są odkręcone oba krany na raz, to w ciągu godziny napełniają
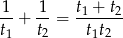
część basenu. Zatem cały basen napełnią w ciągu
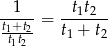
(przez tyle trzeba pomnożyć 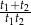 , żeby otrzymać 1, czyli cały basen).
, żeby otrzymać 1, czyli cały basen).
Możemy teraz zapisać podane równania.
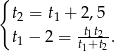
Podstawiamy z pierwszego równania do drugiego i mamy
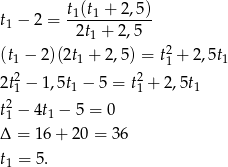
Zatem 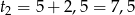 .
.
Sposób II
Oznaczmy przez 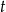 czas potrzebny na napełnienie basenu dwoma kranami. W takim razie pierwszy kran napełnia basen w czasie
czas potrzebny na napełnienie basenu dwoma kranami. W takim razie pierwszy kran napełnia basen w czasie 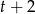 , a drugi w czasie
, a drugi w czasie 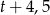 . Wydajność (czyli ile wlewają wody np. w ciągu godziny) dwóch kranów jest sumą wydajności każdego z kranów, co daje równanie.
. Wydajność (czyli ile wlewają wody np. w ciągu godziny) dwóch kranów jest sumą wydajności każdego z kranów, co daje równanie.
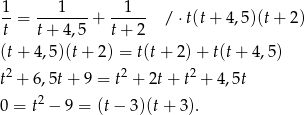
Zatem 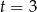 i krany napełniają basen odpowiednio w ciągu
i krany napełniają basen odpowiednio w ciągu 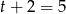 i
i 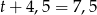 godziny.
godziny.
Odpowiedź: 5 godzin i 7,5 godziny

