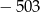Zadanie nr 2392708
Oblicz 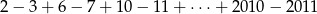 .
.
Rozwiązanie
Sposób I
Liczymy
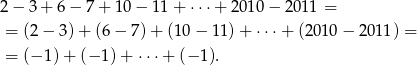
Ile jest tych 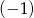 -ek? – tyle ile liczb
-ek? – tyle ile liczb
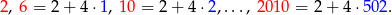
Widać więc, że jest ich 503, czyli interesująca nas suma jest równa -503.
Sposób II
Możemy też liczyć tak:
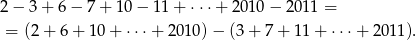
W każdym nawiasie mamy sumę kolejnych wyrazów ciągu arytmetycznego o różnicy 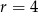 – obliczmy ile jest tych wyrazów. Oczywiście w obu nawiasach jest tyle samo liczb, więc wystarczy zająć się pierwszym nawiasem. Jeżeli
– obliczmy ile jest tych wyrazów. Oczywiście w obu nawiasach jest tyle samo liczb, więc wystarczy zająć się pierwszym nawiasem. Jeżeli 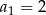 i
i 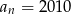 to ze wzoru na
to ze wzoru na  -ty wyraz ciągu arytmetycznego mamy
-ty wyraz ciągu arytmetycznego mamy
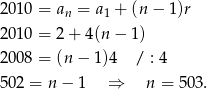
Zatem interesująca nas suma jest równa (korzystamy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego)
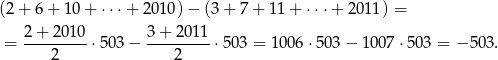
Odpowiedź: