Zadanie nr 5903515
Oblicz sumę wszystkich liczb trzycyfrowych zapisanych wyłącznie za pomocą cyfr wybranych ze zbioru 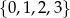 .
.
Rozwiązanie
Sposób I
Zajmijmy się najpierw liczbami, w których jedną z cyfr jest 0. Jeżeli 0 występuje dwukrotnie, to mamy 3 liczby o sumie
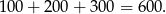
Jeżeli 0 występuje tylko raz i pozostałe cyfry są równe to mamy 6 liczb o sumie
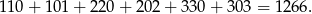
Jeżeli natomiast 0 jest tylko raz, ale pozostałe cyfry są różne, to mamy 12 liczb o sumie
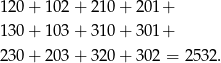
Pozostały nam do rozpatrzenia liczby bez 0. Jeżeli wszystkie cyfry są równe to mamy 3 liczby o sumie
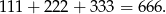
Jeżeli wszystkie cyfry są różne to mamy 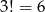 liczb o sumie
liczb o sumie
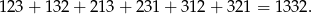
Pozostała nam sytuacja trzech niezerowych liczb, z których dwie są równe. Można łatwo policzyć, że jest 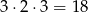 takich liczb (wybieramy której cyfry ma nie być, potem wybieramy, która cyfra ma się powtarzać, a na koniec ustalamy, gdzie ma stać pojedyncza cyfra). Suma tych liczb jest równa
takich liczb (wybieramy której cyfry ma nie być, potem wybieramy, która cyfra ma się powtarzać, a na koniec ustalamy, gdzie ma stać pojedyncza cyfra). Suma tych liczb jest równa
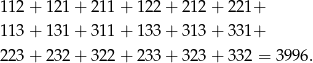
Zatem suma wszystkich liczb jest równa
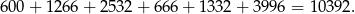
Sposób II
Policzmy najpierw sumę cyfr jedności wszystkich interesujących nas liczb. Dla każdej z cyfr 1,2,3 jest
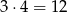
liczb kończących się na tę cyfrę (bo cyfrę setek możemy wybrać na 3, a cyfrę dziesiątek na 4 sposoby). Liczby z zerem na końcu nas nie interesują, bo na razie liczymy tylko sumy cyfr jedności. Tak więc suma cyfr jedności jest równa
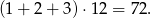
Dokładnie tak samo jest z sumą dziesiątek – jest
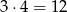
liczb z ustaloną cyfrą dziesiątek, więc suma dziesiątek z wszystkich liczb będzie równa
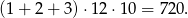
Z cyframi setek jest odrobinę inaczej, bo teraz, przy ustalonej cyfrze setek, jest
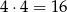
liczb. Suma setek jest więc równa
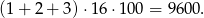
W takim razie suma wszystkich liczb to
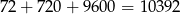
Odpowiedź: 10392

