/Szkoła średnia/Zadania z treścią/Własności liczb/Suma ciągu

Zadanie nr 8271005

Oblicz sumę wszystkich liczb naturalnych trzycyfrowych, które przy dzieleniu przez 7 dają resztę 5.

Wersja PDF

Rozwiązanie

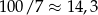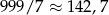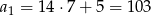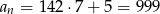Aby znaleźć najmniejszą i największą z tych liczb zauważmy, że 100/7 ≈ 14,3 i 9 99/7 ≈ 142,7 . Zatem najmniejszą liczbą będzie a1 = 14 ⋅7+ 5 = 103 , a największą an = 1 42⋅7 + 5 = 999 .

Liczby te tworzą ciąg arytmetyczny o różnicy 7. Obliczmy, ile ma on wyrazów. Ze wzoru na n –ty wyraz ciągu arytmetycznego mamy

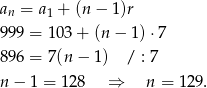
an = a1 + (n − 1)r 999 = 10 3+ (n− 1)⋅7 896 = 7(n − 1) / : 7 n− 1 = 128 ⇒ n = 12 9.

Interesująca nas suma jest więc równa

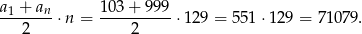
a + a 103 + 999 -1----n-⋅n = ----------⋅1 29 = 551 ⋅129 = 71079. 2 2

 
Odpowiedź: 71 079

Wersja PDF