/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny/Udowodnij...

Zadanie nr 7659894

Dodaj do ulubionych
Dodaj do rozwiązanych

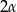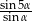Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt 2α , a z ramieniem kąt α . Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy sisinn5αα .

Rozwiązanie

Zaczynamy od rysunku.

PIC

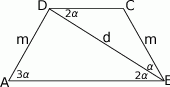
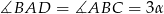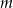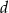Zaznaczyliśmy na rysunku kąt ∡BAD = ∡ABC = 3α . Ponieważ intersujące nas trójkąty mają dwa boki tej samej długości (m i d ), to stosunek ich pól wynosi

1DA ⋅DB sin ∡ADB md sin (180∘ − 5α) sin 5α 21--------------------= -------------------= ------. 2 BC ⋅BD sin∡DBC md sin α sin α
Wersja PDF