/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny/Z przekątną

Zadanie nr 1242797

Dodaj do ulubionych
Dodaj do rozwiązanych

Ramię trapezu równoramiennego 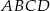ABCD ma długość 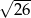√ --- 26 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

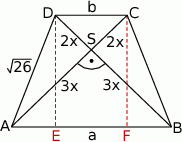
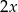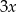Wiemy, że przekątne trapezu dzielą się w stosunku 2:3, więc możemy oznaczyć długości odcinków, na które się dzielą przez 2x i 3x . Stosujemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym ASD .

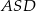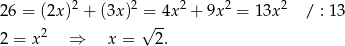
2 6 = (2x)2 + (3x)2 = 4x 2 + 9x2 = 13x 2 / : 13 2 √ -- 2 = x ⇒ x = 2.

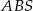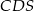Teraz z trójkątów prostokątnych ABS i CDS obliczamy długości podstaw trapezu.

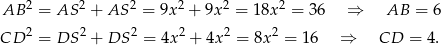
AB 2 = AS 2 + AS 2 = 9x2 + 9x2 = 18x 2 = 36 ⇒ AB = 6 2 2 2 2 2 2 CD = DS + DS = 4x + 4x = 8x = 16 ⇒ CD = 4.

Pole trapezu obliczymy na dwa sposoby.

Sposób I

Pole trapezu obliczamy jako sumę pól czterech trójkątów prostokątnych na które dzielą go przekątne.

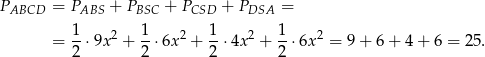
P = P + P + P + P = ABCD ABS BSC CSD DSA = 1⋅ 9x2 + 1-⋅6x2 + 1-⋅4x 2 + 1-⋅6x2 = 9 + 6 + 4 + 6 = 25 . 2 2 2 2

Sposób II

Obliczamy długość wysokości trapezu. Zauważmy najpierw, że

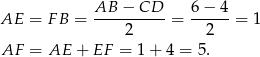
AB--−-CD-- 6-−-4- AE = FB = 2 = 2 = 1 AF = AE + EF = 1+ 4 = 5.

Patrzymy teraz na trójkąt prostokątny 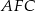AF C .

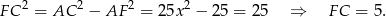
2 2 2 2 FC = AC − AF = 25x − 25 = 25 ⇒ F C = 5.

Pole trapezu jest więc równe

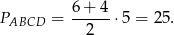
6+ 4 PABCD = ------⋅5 = 25. 2

 
Odpowiedź: 25

Wersja PDF