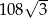/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny/Z przekątną

Zadanie nr 3010094

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie równoramiennym 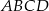ABCD przekątna 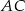AC jest prostopadła do ramienia i tworzy z dłuższą podstawą 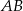AB trapezu kąt o mierze 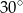30∘ . Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej 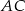AC wynosi 12 √ 3- .

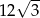Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

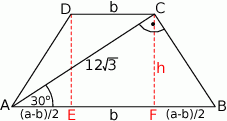
Patrzymy na trójkąty prostokątne 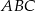ABC i AF C .

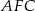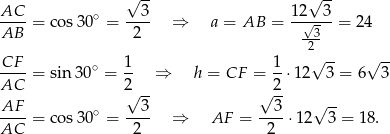
√ -- √ -- AC-- = co s30∘ = --3- ⇒ a = AB = 12√--3 = 24 AB 2 -3- 2 -CF- ∘ 1- 1- √ -- √ -- AC = sin 30 = 2 ⇒ h = CF = 2 ⋅12 3 = 6 3 √ -- √ -- √ -- -AF- = co s30∘ = --3- ⇒ AF = --3-⋅12 3 = 18. AC 2 2

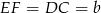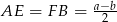Zauważmy jeszcze, że EF = DC = b i a−b-- AE = F B = 2 . Stąd

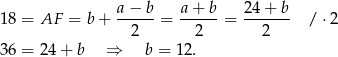
a− b a+ b 24 + b 18 = AF = b+ ------= -----= ------- / ⋅2 2 2 2 36 = 24 + b ⇒ b = 12.

Pozostało obliczyć pole trapezu.

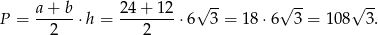
-- -- -- P = a-+-b-⋅h = 24+--12-⋅6√ 3 = 18 ⋅6√ 3 = 108√ 3. 2 2

 
Odpowiedź: √ -- 108 3

Wersja PDF