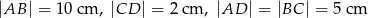Zadanie nr 4930522
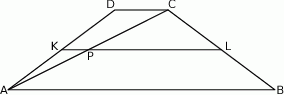
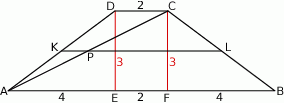
W trapezie równoramiennym  punkty
punkty  i
i  są odpowiednio środkami ramion
są odpowiednio środkami ramion 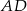 i
i 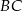 . Przekątna
. Przekątna 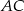 przecina odcinek
przecina odcinek 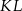 w punkcie
w punkcie 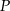 . Wiedząc, że
. Wiedząc, że 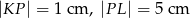 oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
Rozwiązanie
Zauważmy, że odcinek 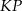 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 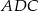 . Zatem
. Zatem
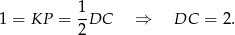
Analogicznie, odcinek 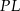 jest odcinkiem łączącym środki boków w trójkącie
jest odcinkiem łączącym środki boków w trójkącie 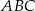 . Zatem
. Zatem
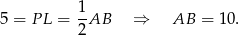
Aby obliczyć długości ramion 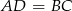 dorysujmy wysokości
dorysujmy wysokości 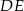 i
i 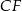 .
.
Zauważmy, że
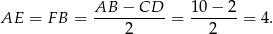
Patrzymy teraz na trójkąt prostokątny 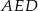 .
.
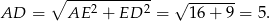
Odpowiedź: