/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny/Z przekątną

Zadanie nr 7797612

W trapezie równoramiennym 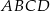ABCD dłuższa podstawa 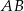AB ma taką samą długość jak jego przekątna 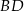BD , a długość krótszej podstawy 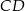CD jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

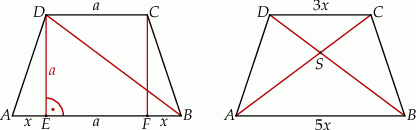
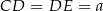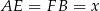Przyjmijmy oznaczenia z rysunku, tzn. CD = DE = a i AE = FB = x .

Piszemy twierdzenie Pitagorasa w trójkącie 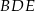BDE .

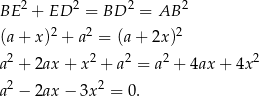
BE 2 + ED 2 = BD 2 = AB 2 2 2 2 (a + x) + a = (a + 2x) a2 + 2ax + x2 + a2 = a 2 + 4ax + 4x2 2 2 a − 2ax − 3x = 0.

Widać, że otrzymane równanie pozwala nam obliczyć 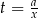t = ax – w tym celu dzielimy je stronami przez x2 .

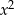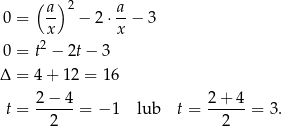
( a) 2 a- 0 = x − 2⋅ x − 3 2 0 = t − 2t− 3 Δ = 4 + 12 = 16 2− 4 2 + 4 t = -----= − 1 lub t = ------= 3. 2 2

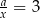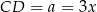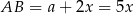Zatem a x = 3 , czyli CD = a = 3x i AB = a + 2x = 5x .

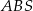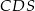Dorysujmy teraz drugą przekątną trapezu (prawy rysunek). Trójkąty ABS i CDS mają równe kąty, więc są podobne. Mamy zatem

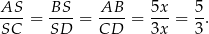
AS--= -BS- = AB-- = 5x- = 5. SC SD CD 3x 3

 
Odpowiedź: 3:5

Wersja PDF