Zadanie nr 9299435
Podstawy trapezu równoramiennego o polu 40 mają długości 6 i 14. Oblicz długość ramienia tego trapezu.
Rozwiązanie
Rozpoczynamy od rysunku.
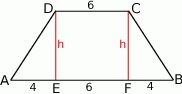
Z podanego pola obliczamy wysokość trapezu
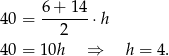
Ponieważ trapez jest równoramienny, długości odcinków 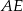 i
i 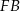 są równe połowie różnicy długości podstaw. Zatem
są równe połowie różnicy długości podstaw. Zatem
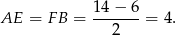
Stosując twierdzenie Pitagorasa w trójkącie 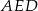 mamy
mamy
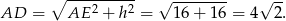
Odpowiedź: