Zadanie nr 9592605
Dany jest trapez prostokątny 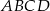 , gdzie
, gdzie 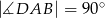 ,
, 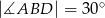 ,
, 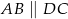 ,
, 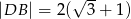 i
i 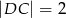 .
.
- Oblicz długość promienia okręgu wpisanego w trójkąt
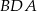 .
. - Wyznacz sumę kwadratów sinusów kątów wewnętrznych trapezu
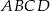 .
.
Rozwiązanie
Zaczynamy od rysunku.
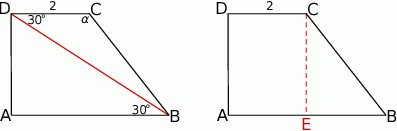
- Obliczmy boki trójkąta
 .
. 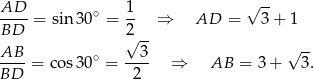
Promień okręgu wpisanego obliczymy ze wzoru na pole
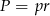 , gdzie
, gdzie 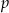 jest połową obwodu trójkąta.
jest połową obwodu trójkąta. 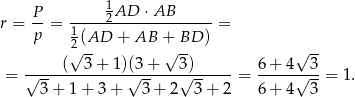
Odpowiedź: 1 -
Sposób I
Z twierdzenia cosinusów w trójkącie
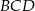 obliczymy długość odcinka
obliczymy długość odcinka 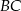 , a to pozwoli nam (z twierdzenia sinusów) obliczyć
, a to pozwoli nam (z twierdzenia sinusów) obliczyć 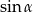 . Liczymy
. Liczymy 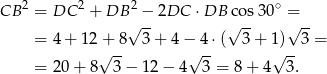
Zatem z twierdzenia sinusów
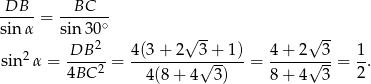
Zatem szukana suma kwadratów sinusów kątów trapezu jest równa.
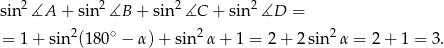
Sposób II
Tym razem obejdziemy się bez twierdzeń cosinusów i sinusów. Dorysujmy wysokość
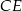 trapezu. Mamy wtedy
trapezu. Mamy wtedy 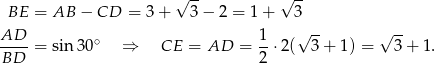
To oznacza, że trójkąt prostokątny
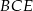 jest równoramienny, więc
jest równoramienny, więc 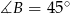 i
i 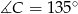 . Interesująca nas suma kwadratów sinusów jest więc równa
. Interesująca nas suma kwadratów sinusów jest więc równa 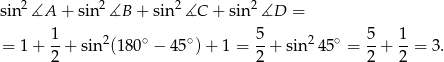
Odpowiedź: 3

