Zadanie nr 8241579

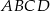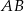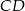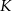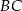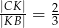Na okręgu o danym promieniu opisano trapez równoramienny ABCD o dłuższej podstawie i krótszej . Punkt styczności dzieli ramię tak, że |CK-|= 2 |KB | 3 .

Wyznacz długość ramienia tego trapezu.
Oblicz cosinus kąta .

Wersja PDF

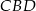Rozwiązanie

Zaczynamy oczywiście od rysunku.

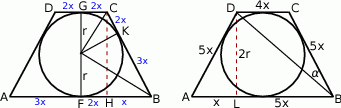
Jeżeli oznaczymy 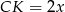i 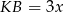, to z faktu, że odcinki stycznych poprowadzonych z punktu do okręgu są równe, mamy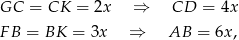
$GC = CK = 2x ⇒ CD = 4x F B = BK = 3x ⇒ AB = 6x,$

gdzie 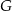i 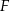są odpowiednimi punktami styczności okręgu z podstawami trapezu. Jeżeli poprowadzimy wysokość 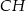, to mamy

$F H = GC = 2x ⇒ HB = 3x − 2x = x.$

Znamy zatem wszystkie boki trójkąta prostokątnego 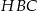i możemy zastosować twierdzenie Pitagorasa.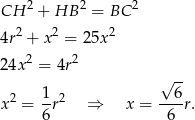

$CH 2 + HB 2 = BC 2 2 2 2 4r + x = 2 5x 24x 2 = 4r2 √ -- 2 1-2 --6- x = 6r ⇒ x = 6 r.$

Zatem ramię ma długość

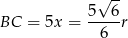
$√ -- 5--6- BC = 5x = 6 r$

Odpowiedź: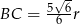
Żądany cosinus obliczymy z twierdzenia cosinusów w trójkącie 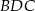. Zanim jednak to zrobimy, musimy wyliczyć długość przekątnej 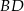. Patrzymy na trójkąt prostokątny 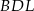i mamy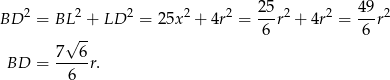
$25 49 BD 2 = BL 2 + LD 2 = 2 5x2 + 4r2 = ---r2 + 4r 2 =--r2 √ -- 6 6 7 6 BD = -6--r.$

Teraz stosujemy twierdzenie cosinusów w trójkącie .

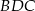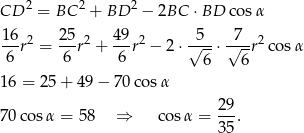
$CD 2 = BC 2 + BD 2 − 2BC ⋅BD cos α 16 25 49 5 7 ---r2 = --r2 + ---r2 − 2⋅√---⋅ √--r2co sα 6 6 6 6 6 16 = 25 + 4 9− 7 0cos α 70co sα = 58 ⇒ co sα = 29. 35$

Odpowiedź: