Zadanie nr 1502808
W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość  , druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
, druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku.
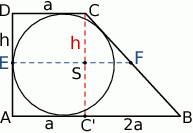
Druga część zadania jest bardzo łatwa. Szukany odcinek 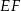 jest równoległy do podstaw (tw. Talesa) i składa się z dwóch części: odcinka
jest równoległy do podstaw (tw. Talesa) i składa się z dwóch części: odcinka 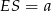 oraz
oraz 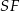 , który jest równy połowie
, który jest równy połowie 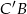 (np. z podobieństwa trójkątów
(np. z podobieństwa trójkątów 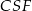 i
i 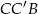 lub z twierdzenia Talesa), czyli też
lub z twierdzenia Talesa), czyli też  . Zatem
. Zatem
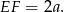
Jeżeli ktoś lubi różne wzorki, to w dowolnym trapezie o podstawach  i
i 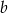 odcinek łączący środki ramion ma długość
odcinek łączący środki ramion ma długość 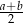 . Oczywiście zgadza się to z naszymi wyliczeniami.
. Oczywiście zgadza się to z naszymi wyliczeniami.
Aby obliczyć pole trapezu, musimy wyznaczyć jego wysokość 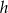 . Na mocy twierdzenia Pitagorasa zastosowanego do trójkąta
. Na mocy twierdzenia Pitagorasa zastosowanego do trójkąta 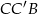 mamy
mamy
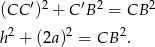
Ponadto, musimy w końcu wykorzystać fakt, że trapez jest opisany na okręgu. Oznacza to, że sumy przeciwległych boków są równe (ta własność w pełni charakteryzuje czworokąty opisane na okręgu, co warto zapamiętać). Zatem
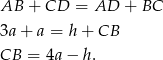
Podstawiając tę wartość do wcześniej napisanego twierdzenia Pitagorasa otrzymujemy
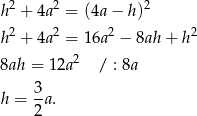
Możemy więc policzyć pole
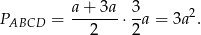
Odpowiedź: Pole: 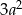 , odcinek:
, odcinek: