/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Kąty, funkcje trygonometryczne

Zadanie nr 4684801

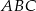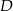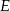Dany jest trójkąt prostokątny równoramienny ABC . Punkty D i E dzielą przeciwprostokątną 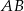AB na trzy odcinki równej długości. Oblicz cosinus kąta DCE .

Wersja PDF

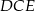Rozwiązanie

Oznaczmy 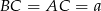BC = AC = a .

PIC

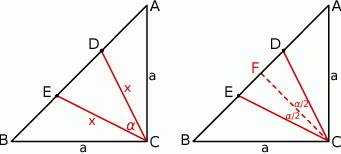
Wtedy oczywiście 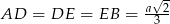√ - AD = DE = EB = a32- .

Sposób I

Żądany 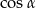co sα możemy obliczyć z twierdzenia cosinusów w trójkącie równoramiennym 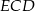ECD , ale najpierw musimy obliczyć długości jego ramion 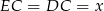EC = DC = x . Rozpoczynamy więc od twierdzenia cosinusów w trójkącie EBC .

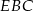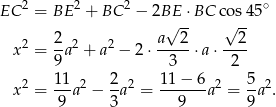
EC 2 = BE 2 + BC 2 − 2BE ⋅ BC cos 45∘ √ -- √ -- x2 = 2a2 + a2 − 2⋅ a--2-⋅a⋅ --2- 9 3 2 2 11-2 2- 2 11-−-6- 2 5-2 x = 9 a − 3a = 9 a = 9a .

Piszemy teraz twierdzenie cosinusów w trójkącie 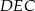DEC .

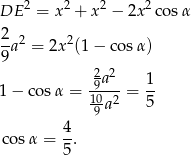
DE 2 = x 2 + x 2 − 2x 2cos α 2 -a 2 = 2x2(1 − cos α) 9 29a2 1 1− cosα = 10-2-= -- 9 a 5 4- co sα = 5.

Sposób II

Niech 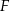F będzie środkiem przeciwprostokątnej 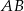AB . Ponieważ trójkąt 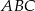ABC jest połówką kwadratu, mamy

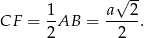
√ -- 1- a--2- CF = 2AB = 2 .

Odcinek 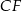CF zawiera się w dwusiecznej kąta 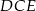DCE , więc korzystając z trójkąta prostokątnego 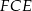FCE możemy bardzo łatwo obliczyć tangens kąta α 2 .

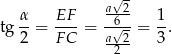
a√-2- tg α-= EF--= -√6- = 1. 2 FC a-2- 3 2

Znając tangens, łatwo obliczyć cosinus.

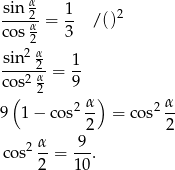
sin α 1 ----2α-= -- / ()2 cos 2 3 sin2 α 1 ---2-2α = -- co(s 2 9 ) 2 α- 2 α- 9 1− cos 2 = cos 2 α 9 co s2--= ---. 2 10

Teraz pozostało skorzystać ze wzoru 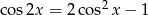2 co s2x = 2 cos x− 1 . Mamy zatem

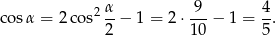
2 α 9 4 cos α = 2 cos -2 − 1 = 2 ⋅10-− 1 = 5.

 
Odpowiedź: 4 5

Wersja PDF