/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Kąty, funkcje trygonometryczne

Zadanie nr 6261966

Dodaj do ulubionych
Dodaj do rozwiązanych

Sprawdź, czy trójkąt o bokach: 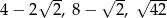√ -- √ --√ --- 4 − 2 2, 8− 2, 42 jest trójkątem prostokątnym.

Rozwiązanie

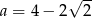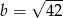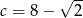Na mocy twierdzenia Pitagorasa wystarczy sprawdzić, czy kwadrat największej z danych liczb jest równy sumie kwadratów dwóch pozostałych. Oznaczmy √ -- a = 4 − 2 2 , √ --- b = 42 i √ -- c = 8 − 2 . Mamy zatem

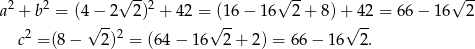
√ -- √ -- √ -- a2 + b 2 = (4− 2 2)2 + 42 = (16 − 16 2 + 8 )+ 42 = 66 − 16 2 2 √ -- 2 √ -- √ -- c =(8 − 2 ) = (64− 16 2 + 2) = 66 − 1 6 2.

Zatem rzeczywiście 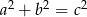a2 + b 2 = c2 , czyli trójkąt jest prostokątny.  
Odpowiedź: Tak, jest prostokątny.

Wersja PDF