Zadanie nr 8859518
Trapez równoramienny jest opisany na okręgu. Suma długości krótszej podstawy i ramienia trapezu jest równa 30. Wyraź pole tego trapezu jako funkcję długości jego ramienia. Wyznacz dziedzinę tej funkcji.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
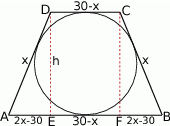
Jeżeli oznaczymy długość ramienia przez  , to krótsza podstawa ma długość
, to krótsza podstawa ma długość 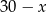 . Ponieważ będzie nas interesować jakie wartości może przyjmować
. Ponieważ będzie nas interesować jakie wartości może przyjmować  (dziedzina szukanej funkcji), zauważmy, że w tym miejscu musimy mieć
(dziedzina szukanej funkcji), zauważmy, że w tym miejscu musimy mieć 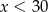 i jednocześnie
i jednocześnie  może być dowolnie bliskie 30 (skraca się krótsza podstawa).
może być dowolnie bliskie 30 (skraca się krótsza podstawa).
Wiadomo, że w czworokącie opisanym na okręgu sumy przeciwległych boków są równe. W naszym trapezie są one równe 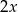 (suma długości ramion), więc dłuższa podstawa musi mieć długość:
(suma długości ramion), więc dłuższa podstawa musi mieć długość:
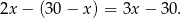
Znamy sumę podstaw trapezu, pozostało nam więc wyliczyć długość jego wysokości. Zrobimy to z trójkąta prostokątnego 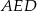 .
.
Ponieważ 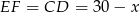 , odcinki
, odcinki 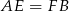 muszą mieć długość
muszą mieć długość
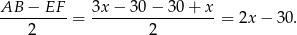
Zauważmy, że ten wzór daje nam kolejne ograniczenie na  :
: 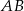 ma być dłuższą podstawą, czyli
ma być dłuższą podstawą, czyli
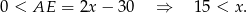
Jednocześnie powinno być jasne, że  może być dowolnie blisko 15 (dla
może być dowolnie blisko 15 (dla 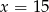 dostajemy kwadrat).
dostajemy kwadrat).
Liczymy wysokość
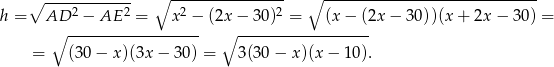
Zatem pole jest równe
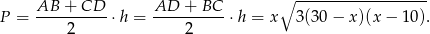
Jak już ustaliliśmy po drodze, dziedziną tej funkcji jest przedział 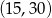 .
.
Odpowiedź: 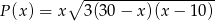 ,
,