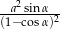/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny opisany na okręgu/Pole

Zadanie nr 5739327

Dodaj do ulubionych
Dodaj do rozwiązanych

Na okręgu opisano trapez, w którym krótsza podstawa ma długość a , a dłuższa podstawa tworzy z ramionami kąty o mierze α . Oblicz pole tego trapezu.

Rozwiązanie

Oznaczmy długość dłuższej podstawy przez 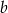b i długość ramienia przez d .

PIC

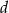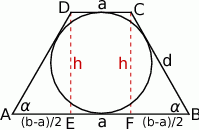
Z podanych informacji wynika, że trapez jest równoramienny oraz

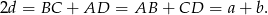
2d = BC + AD = AB + CD = a+ b.

Ponadto

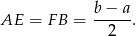
AE = F B = b-−-a-. 2

Patrzymy teraz na trójkąt prostokątny CF B . Mamy w nim

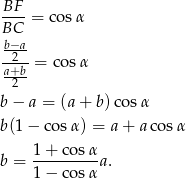
BF ---= cos α BC b−2a- a+b-= co sα 2 b − a = (a + b) cosα b(1 − co sα) = a + a cosα 1+--cosα- b = 1− cosα a.

Do obliczenia pola brakuje nam jeszcze wysokości trapezu. Można ją obliczyć z trójkąta prostokątnego 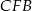CF B – my jednak zamiast ją obliczać wyrazimy ją w zależności od 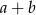a+ b , a wartość tego wyrażenia i tak musimy obliczyć licząc pole.

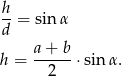
h --= sin α d h = a-+-b-⋅sinα . 2

Pole trapezu jest więc równe

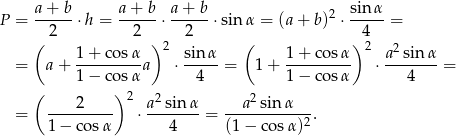
P = a+--b⋅h = a-+-b-⋅ a-+-b-⋅sinα = (a+ b)2 ⋅ sin-α-= 2 2 2 4 ( 1 + cos α ) 2 sinα ( 1+ cosα ) 2 a 2sin α = a + ---------a ⋅-----= 1+ --------- ⋅--------= 1 − cos α 4 1− cosα 4 ( 2 ) 2 a2sin α a2sin α = --------- ⋅--------= ----------2-. 1 − co sα 4 (1− cosα)

 
Odpowiedź: --a2sinα-- (1−cosα)2

Wersja PDF