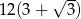/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny opisany na okręgu/Pole

Zadanie nr 8043601

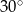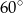W trapezie opisanym na okręgu kąty przy dłuższej podstawie mają miary ∘ 30 i 6 0∘ , a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

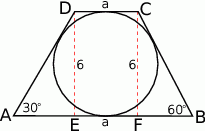
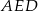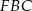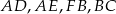Z trójkątów prostokątnych AED i F BC możemy powyliczać długości odcinków AD ,AE ,FB ,BC .

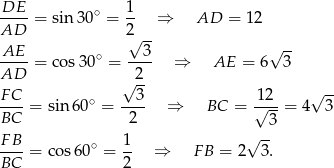
DE-- = sin 30∘ = 1- ⇒ AD = 12 AD 2 -- AE √ 3 √ -- ---- = co s30∘ = ---- ⇒ AE = 6 3 AD √ 2- F-C- ∘ --3- 1-2- √ -- BC = sin 60 = 2 ⇒ BC = √ --= 4 3 √ -3 F-B-= cos6 0∘ = 1- ⇒ FB = 2 3. BC 2

Skorzystamy teraz z faktu, że jeżeli czworokąt jest opisany na okręgu to sumy przeciwległych boków są równe. Oznaczając 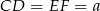CD = EF = a mamy

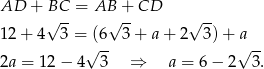
AD + BC = AB + CD √ -- √ -- √ -- 12 + 4 3 = (6 3+ a+ 2 3)+ a 2a = 12 − 4 √ 3- ⇒ a = 6 − 2√ 3.

Zatem podstawy mają długości

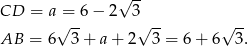
√ -- CD = a =√-6 − 2 3√ -- √ -- AB = 6 3+ a+ 2 3 = 6 + 6 3.

Pole trapezu jest równe

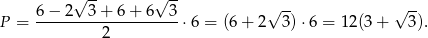
√ -- √ -- 6− 2 3+ 6+ 6 3 √ -- √ -- P = --------------------⋅6 = (6 + 2 3) ⋅6 = 12 (3+ 3). 2

 
Odpowiedź: Podstawy: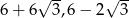 √ -- √ -- 6+ 6 3,6 − 2 3 , pole: √ -- 12(3 + 3 )

Wersja PDF