Zadanie nr 2998344
Czworokąt 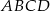 jest trapezem o podstawach
jest trapezem o podstawach 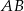 i
i 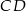 . Wykaż że
. Wykaż że
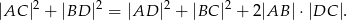
Rozwiązanie
Przyjmijmy oznaczenia z poniższego rysunku.
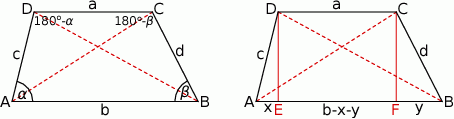
Sposób I
Na powyższym rysunku mamy cztery trójkąty, z których możemy obliczyć długości przekątnych trapezu: 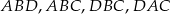 . Piszemy w każdym z tych trójkątów twierdzenie cosinusów
. Piszemy w każdym z tych trójkątów twierdzenie cosinusów
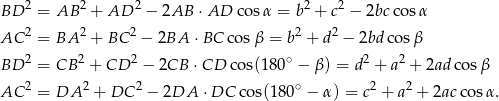
Teraz, żeby pozbyć się wszystkich cosinusów dodajemy te równości stronami, przy czym pierwsze dwie mnożymy przez  , a dwie ostatnie przez
, a dwie ostatnie przez 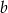 . Mamy zatem
. Mamy zatem
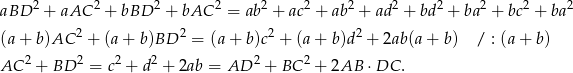
Sposób II
Tym razem obejdziemy się bez twierdzenia cosinusów. Dorysujmy wysokości 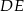 i
i 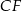 trapezu i niech
trapezu i niech 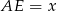 ,
, 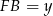 . Stosując twierdzenie Pitagorasa w trójkątach
. Stosując twierdzenie Pitagorasa w trójkątach 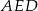 i
i 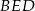 mamy
mamy
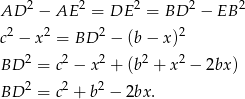
Analogicznie, stosując twierdzenie Pitagorasa w trójkątach 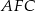 i
i 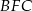 mamy
mamy
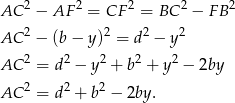
Mamy zatem