/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny/Udowodnij...

Zadanie nr 5309071

Przekątne trapezu 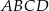ABCD przecinają się w punkcie 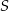S . Promień okręgu opisanego na trójkącie ostrokątnym 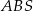ABS jest o 1 większy od promienia okręgu opisanego na trójkącie 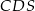CDS , a długości podstaw trapezu spełniają warunek 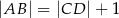|AB | = |CD | + 1 . Wykaż, że

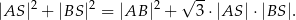
√ -- |AS |2 + |BS |2 = |AB |2 + 3⋅|AS |⋅ |BS |.
Wersja PDF

Rozwiązanie

Zaczynamy naturalnie od rysunku.

PIC

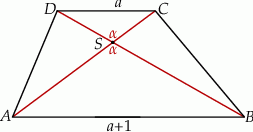
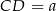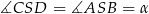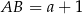Jeżeli oznaczymy CD = a i ∡CSD = ∡ASB = α , to AB = a + 1 i na mocy twierdzenia sinusów mamy

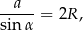
a ----- = 2R , sin α

gdzie przez 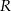R oznaczyliśmy promień okręgu opisanego na trójkącie 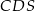CDS . Z założenia, promień okręgu opisanego na trójkącie 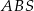ABS jest równy 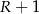R + 1 , więc

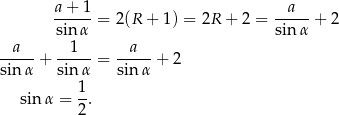
a-+-1-= 2(R + 1) = 2R + 2 = -a---+ 2 sin α sin α a 1 a -----+ -----= -----+ 2 sin α sin α sinα sin α = 1. 2

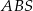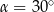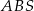Wiemy, że trójkąt ABS jest ostrokątny, więc ∘ α = 30 . Piszemy teraz twierdzenie cosinusów w trójkącie ABS .

√ -- AB 2 = AS 2 + BS2 − 2AS ⋅BS cos α = AS 2 + BS 2 − 2AS ⋅ BS ⋅--3- 2 2 √ -- 2 2 AB + AS ⋅BS ⋅ 3 = AS + BS .
Wersja PDF