Zadanie nr 3289877
Podstawy trapezu 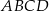 mają długości
mają długości 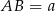 i
i 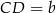 . Oblicz długość odcinka łączącego środki ramion trapezu.
. Oblicz długość odcinka łączącego środki ramion trapezu.
Rozwiązanie
Sposób I
Dorysowujemy odcinek 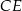 równoległy do
równoległy do 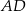 .
.
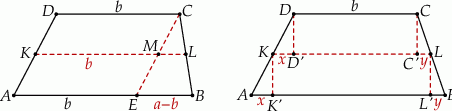
Odcinek 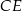 podzielił odcinek
podzielił odcinek 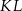 na dwie części, przy czym
na dwie części, przy czym 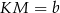 , a odcinek
, a odcinek 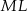 łączy środki boków w trójkącie
łączy środki boków w trójkącie 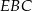 . Zatem
. Zatem
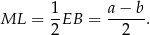
Stąd
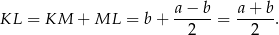
Sposób II
Niech 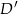 i
i 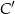 będą rzutami punktów
będą rzutami punktów 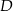 i
i 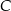 na prostą
na prostą 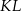 , a
, a 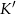 i
i 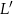 niech będą rzutami punktów
niech będą rzutami punktów 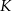 i
i 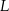 na prostą
na prostą 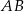 . Trójkąty
. Trójkąty 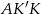 i
i 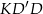 są przystające, zatem
są przystające, zatem 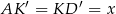 . Analogicznie z przystawania trójkątów
. Analogicznie z przystawania trójkątów 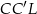 i
i 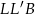 mamy
mamy 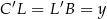 . Mamy zatem
. Mamy zatem
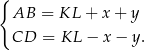
Dodając te dwie równości stronami mamy
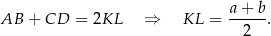
Sposób III
Dorysujmy drugą kopię trapezu odbijając wyjściowy trapez w symetrii względem środka ramienia 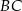 .
.
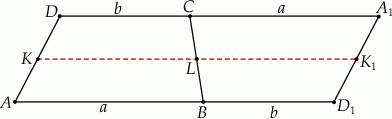
Otrzymamy w ten sposób równoległobok o podstawie 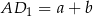 , w którym odcinek
, w którym odcinek 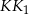 łączy środki ramion
łączy środki ramion 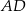 i
i 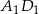 . Odcinek ten jest dwa razy dłuższy od interesującego nas odcinka
. Odcinek ten jest dwa razy dłuższy od interesującego nas odcinka 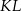 . Zatem
. Zatem
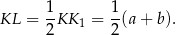
Sposób IV
Zauważmy, że
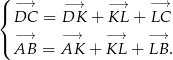
Dodając te dwie równości stronami mamy
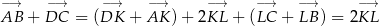
Ponieważ wektory 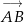 i
i 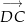 są równoległe i mają ten sam zwrot powyższa równość oznacza, że
są równoległe i mają ten sam zwrot powyższa równość oznacza, że
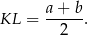
Sposób V
Jeżeli trapez jest równoległobokiem, to zadanie jest banalne, więc przyjmijmy, że ramiona trapezu przecinają się w punkcie 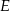 oraz oznaczmy
oraz oznaczmy 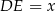 ,
, 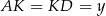 .
.
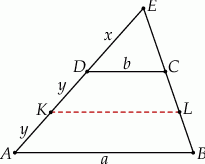
Z podobieństw trójkątów 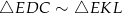 i
i 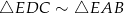 mamy
mamy
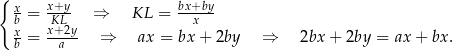
Podstawiając teraz z drugiej równości 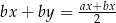 do pierwszej mamy
do pierwszej mamy
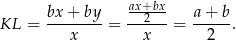
Odpowiedź: