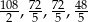Zadanie nr 3679992
W trapezie o podstawach długości 12 cm i 8 cm oraz wysokości równej 6 cm poprowadzono przekątne, które podzieliły go na cztery trójkąty. Oblicz pole każdego z otrzymanych trójkątów.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
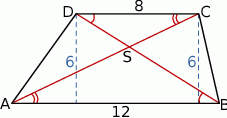
Obliczmy najpierw pola trójkątów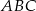 
i 
.
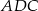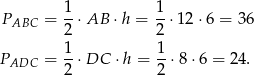
Jedną z najważniejszych własności trapezu, która jest notorycznie wykorzystywana w zadaniach, jest podobieństwo trójkątów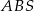 
i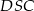 
(mają równe kąty). W dodatku, skala podobieństwa to dokładnie stosunek długości podstaw. W szczególności
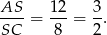
To oznacza, że znamy stosunek pól trójkątów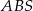 
i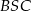 
(bo trójkąty te mają wspólną wysokość opuszczoną z wierzchołka 
)
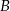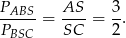
Stąd
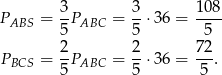
Analogicznie
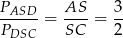
oraz
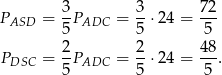
Odpowiedź: 
