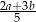Zadanie nr 9062452
Połączono ramiona trapezu odcinkiem równoległym do podstaw i dzielącym te ramiona w stosunku 2:3 licząc od krótszej podstawy. Oblicz długość tego odcinka, jeśli wiesz, że podstawy trapezu mają długości  i
i 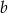 , gdzie
, gdzie 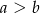 .
.
Rozwiązanie
Zacznijmy od rysunku.
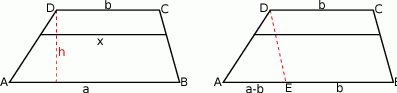
Sposób I
Poprowadzony odcinek podzieli wysokość 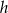 trapezu na odcinki długości
trapezu na odcinki długości 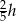 i
i 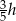 . Możemy więc policzyć pole trapezu dodając do siebie pola utworzonych trapezów.
. Możemy więc policzyć pole trapezu dodając do siebie pola utworzonych trapezów.
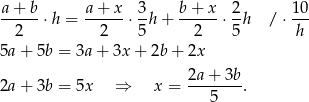
Sposób II
Jeżeli poprowadzimy odcinek 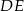 równoległy do ramienia
równoległy do ramienia 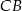 , to szukany odcinek zostanie podzielony na dwa, jeden o długości
, to szukany odcinek zostanie podzielony na dwa, jeden o długości 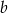 , a drugi o długości
, a drugi o długości 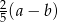 (twierdzenie Talesa lub podobieństwo). Zatem ma on długość
(twierdzenie Talesa lub podobieństwo). Zatem ma on długość
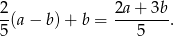
Odpowiedź: