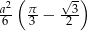Zadanie nr 2757699
Ze środka ciężkości trójkąta równobocznego o boku  , wykreślono okrąg o promieniu
, wykreślono okrąg o promieniu 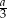 . Oblicz pole części koła nie należącego do trójkąta.
. Oblicz pole części koła nie należącego do trójkąta.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
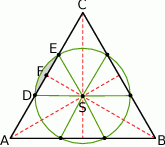
Przyjrzyjmy się trójkątowi równoramiennemu 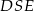 . Uzasadnimy, że jest on równoboczny – można to zrobić na wiele różnych sposobów, my użyjemy funkcji trygonometrycznych. Zauważmy, że
. Uzasadnimy, że jest on równoboczny – można to zrobić na wiele różnych sposobów, my użyjemy funkcji trygonometrycznych. Zauważmy, że
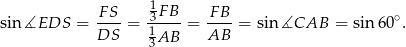
Ponieważ kąt 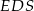 jest ostry (jako kąt przy podstawie trójkąta równoramiennego) mamy stąd
jest ostry (jako kąt przy podstawie trójkąta równoramiennego) mamy stąd
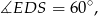
co oznacza, że trójkąt równoramienny 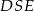 jest równoboczny. Inne możliwe sposoby uzasadnienia tej obserwacji to np. obliczenie długości odcinka
jest równoboczny. Inne możliwe sposoby uzasadnienia tej obserwacji to np. obliczenie długości odcinka 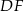 z twierdzenia Pitagorasa w trójkącie
z twierdzenia Pitagorasa w trójkącie 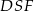 , albo zauważenie, że punkty dzielące boki trójkąta równobocznego na odcinki długości
, albo zauważenie, że punkty dzielące boki trójkąta równobocznego na odcinki długości 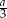 są wierzchołkami sześciokąta foremnego, którego wierzchołki leżą na interesującym nas okręgu.
są wierzchołkami sześciokąta foremnego, którego wierzchołki leżą na interesującym nas okręgu.
Wycinek koła odpowiadający kątowi 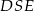 ma pole
ma pole
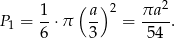
To oznacza, że odcinek koła odpowiadający temu samemu kątowi (tzn. obszar zacieniowany na rysunku) ma pole
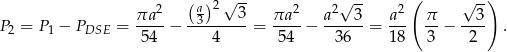
Pole interesującego nas obszaru jest 3 razy większe, więc wynosi
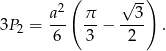
Odpowiedź: